Próvtalsstigar
Eftir Olav Absalonsen í miðnámsrit 4, desember 2014
Tann nýggi 7-trinstigin, sum frammanundan varð settur í gildi í fólkaskúlanum, kom í gildi á miðnámi í 2013. Møguligt var annars at velja ein bókstavsstiga fyri at gera upp við siðvenjuna at rokna villleiðandi miðaltøl í prógvum, sum hevur óhepnar avleiðingar fyri undirvísing og læring.
Tann nýggi 7-trinstigin er gjørdur eftir europeiska ECTS stiganum, sum er ein bókstavsstigi, og hesir eru samanbornir í talvu 1. Tann nýggi 7-trinstigin er gjørdur við tí fyri eyga at gera tað lættari at umseta próvtøl til ECTS stigan, enn tað er við 13-stiganum. Ein spurningur er tí, hví tann nýggi stigin er í tølum og ikki bókstavum. Orsøkin skal vera, at tað skal bera til at rokna eitt miðaltal út.
Talva 1: Samanbering av ECTS og 7-trinstiganum
| ECTS | A | B | C | D | E | Fx | F |
| 7-trinstigin | 12 | 10 | 7 | 4 | 02 | 00 | -3 |
Ein próvtalsstigi er ein skali við intervallum sum til dømis teir, ið verða brúktir til at máta vekt, longd, tíð og hita. Men próvtalsstigar ella próvstavsstigar (ein karakterstigi kann eisini vera í bókstavum) verða brúktir til at umseta metingar um avrik hjá næmingum til eitt tal (ella ein bókstav). Ein slík umseting er altíð ein avrunding, og tá ið tú skalt rokna eitt miðaltal av fleiri mátingum, so skalt tú ikki runda mátingarnar ov nógv av, tí tað ger, at miðaltalið verður skeivt. Í so máta hevur 7-trinstigin sama veikleika sum 13-stigin; hann er bara verri, tí hann hevur færri met at velja í, og tí verða avrundingarnar í miðal størri. Hetta fyribrigdi kallar Peter Knight ’misnýtsla av tølum’, tí at umsetingin av einari meting um eitt avrik til eitt tal er útsett fyri manipulatión, sum er lýst við dømum í hesi greinini.
Spyrja vit, hví ECTS-stigin brúkar bókstavar og ikki tøl, er svarið, at tað er fyri at tað skal ikki bera til at rokna eitt miðaltal út, tí at hesi met eru avrundaðar ásetingar av metingum (um onkur kortini hevði funnið upp á at rokna eitt miðaltal av bókstavum, so hevði hann sett tøl á bókstavarnar og helst roknað við líka stórum intervallum millum bókstavarnar).
Samanbering við 13-stigan
Myndugleikar og skúlar, sum brúka 7-trinstigan, samanbera hann við 13-stigan, sum víst í talvu 2. Av tí at báðir stigarnir verða brúktir til at rokna miðaltøl, kann talva 2 eftirkannast at vita, um hon samsvarar við linjubeina umrokning (sum til dømis umrokning millum stig Celsius og stig Fahrenheit). Talva 3 vísir hesa samanbering.
Talva 2: Almenn samanbering av 13-stiganum og 7-trinstiganum
| 13-stigin | 13 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 03 | 00 |
| 7-trinstigin | 12 | 10 | 7 | 4 | 02 | 00 | -3 |
Talva 3: Samanbering av 13-stiganum og 7-trinstiganum við miðaltølum í huga
| 13-stigin | 11 | 10 | 8½ | 7 | 6 | 5 | 3½ |
| 7-trinstigin | 12 | 10 | 7 | 4 | 02 | 00 | -3 |
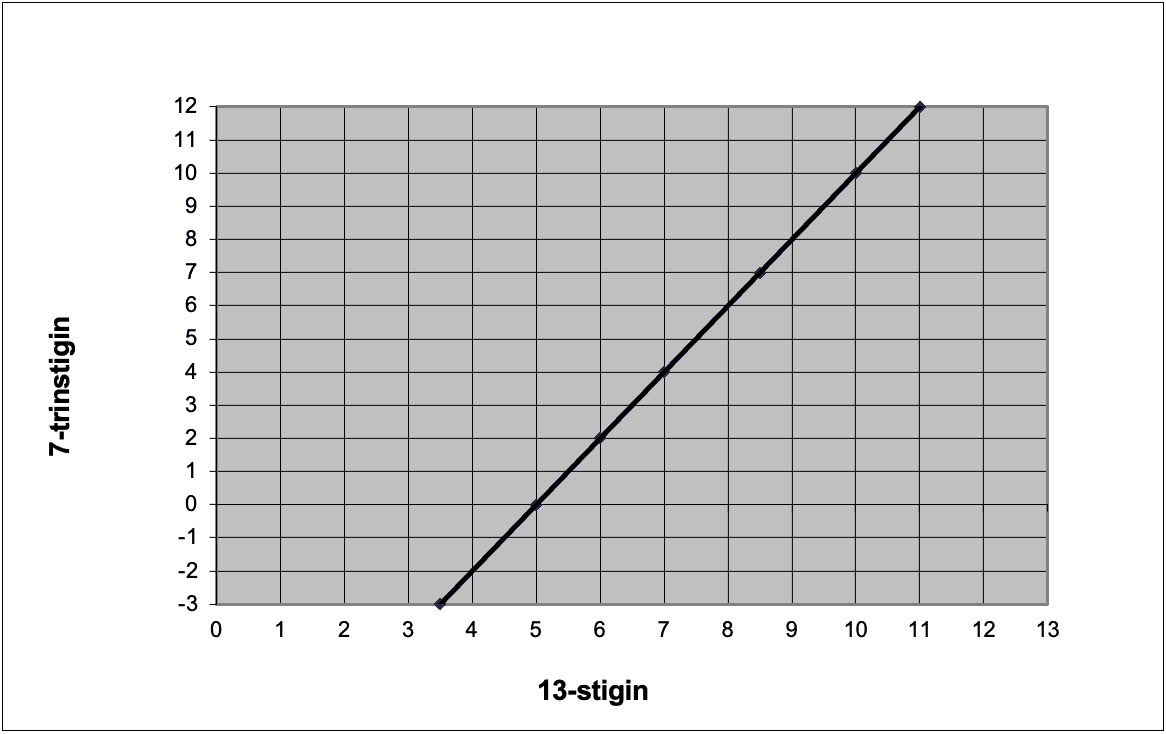
Talva 3 er tann linjubeina samanberingin millum stigarnar báðar og sigur tað sama sum mynd 1, har 13-stigin gongur frá 11 niður í 3½, ið svarar til -3 í nýggja stiganum. Av tí at samanberingin er linjubein, svarar 8½ í 13-stiganum til 7 í tí nýggja. Talva 3 samsvarar ikki við talvu 2, sum er ein almenn samanbering, og tað avdúkar, at 5 av 7 metum samsvara við met á 13-stiganum, at 13 og 00 í 13-stiganum eru ikki til í 7-trinstiganum, at 7 svarar til 8½ á 13-stiganum, og at –3 svarar til 3½ á 13-stiganum, og ikki 00, sum tann fyrra talvan sigur. Tá ið tað snýr seg um at rokna miðaltøl, er –3 eitt frægari met enn 03 í 13-stiganum er, fyri ikki at tala um 00. Tann almenna samanberingin av hesum báðum próvtalsstigum (talva 2) er støddfrøðiliga skeiv og villleiðandi, tá ið miðaltøl skulu roknast. Umrokningar millum stigarnar kunnu verða gjørdar soleiðis (talva 3):
- Frá 13-stiganum til 7-trinstigan: falda við 2 og drag 10 frá.
- Frá 7-trinstiganum til 13-stigan: legg 10 afturat og dividera við 2.
Hesin umrokningarháttur er sum at rokna um millum Fahrenheit og Celsius, og umrokningin samsvarar væl við eina talvu í Uddannelsesguiden.dk, sum danska undirvísingarministeriið gav út í sambandi við upptøku av næmingum á hægri lærustovnar í Danmark í 2008, og ikki við ta almennu samanberingina av einstøku próvtølunum (talva 2). Tann linjubeina samanberingin av próvtalsstigunum er lýst í mynd 1.
Niðanfyri eru tvey dømi, har eitt miðaltal eftir 13-stiganum ikki hevði samsvarað við miðaltalið eftir 7-trinstiganum, soleiðis at tað ikki hevði ligið á linjuni í mynd 1, tí at talan er um ymiskar avrundingar av avrikum til met í báðum stigunum:
Dømi 1
Ein næmingur fær hesi met eftir 13-stiganum: 10, 8, 7, 6, 5 og 03. Hetta gevur 6,5 í miðal, um øll metini viga líka nógv:
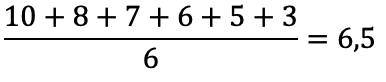
Eftir 7-trinstiganum høvdu metini verið: 10, 7, 4, 02, 00 og 00. Hetta er í miðal 3,8:
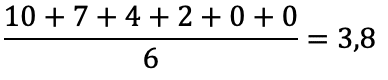
Ella 3,3, um 03 verður umsett til -3:
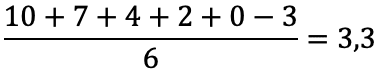
Men tað skuldi verið 3,0, sum er 6,5 eftir 13-stiganum, tá ið linjubein umrokning verður brúkt. Munurin kemur av, at 7 í 7-trinstiganum er hægri enn 8 í 13-stiganum, og 00 í 7-trinstiganum er nógv hægri enn 03 í 13-stiganum (-3 er eisini hægri enn 03 í 13-stiganum).
Mynd 1: 7-trinstigin sum funktión av 13-stiganum.
Dømi 2
Ein annar næmingur fær hesi met eftir 13-stiganum: 8, 7, 6, 6, 5 og 03. Hetta gevur 5,8 í miðal, um øll metini viga líka nógv:
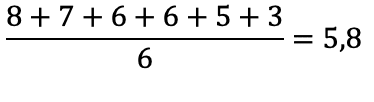
Eftir 7-trinstiganum høvdu metini verið: 7, 4, 02, 02, 00 og 00, um 03 í 13-stiganum svarar til 00 í 7-trinstiganum. Hetta gevur 2,5 í miðal:
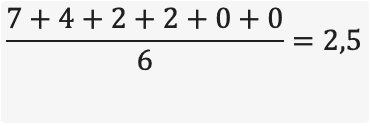
Um 03 í 13-stiganum verður umsett til –3 í 7-trinstiganum, verður miðaltalið 2,0:
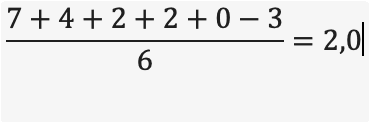
Í hesum dømi hevði næmingurin ikki fingið prógv eftir 13-stiganum, men eftir 7-trinstiganum hevði hann klárað tað við hjálp av avrundingum – ella ‘misnýtslu av tølum’, sum Peter Knight kallar slíkan framferðarhátt.
Sjálvt um 5 met í 7-trinstiganum svara til 5 met á 13-stiganum, eru intervallini ikki eins, sum talva 4 vísir. Til dømis skuldi eitt stórt 9-tal eftir 13-stiganum verið 10 eftir 7-trinstiganum, og eitt lítið 8-tal eftir 13-stiganum skuldi verið 4 eftir 7-trinstiganum. Eisini sæst, at markið millum 5 og 03 á 13-stiganum er lægri enn markið millum 00 og –3 á 7-trinstiganum. Intervallini eru lýst í talvu 4. Hvørki 13 ella 00 í 13-stiganum eru við í talvuni, tí í 7-trinstiganum eru hesir karakterir uttan fyri samanbering, sum mynd 1 vísir.
Talva 4: Samanbering av 13-stiganum og 7-trinstiganum við intervallum
| 13-stigin | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 03 | |||
| 7-trinstigin | 12 | 10 | 7 | 4 | 02 | 00 | -3 | ||||
Tann mest týðandi munurin millum próvtalsstigarnar er í niðasta próvtalinum –3, sum her er sett at svara til 03 í 13-stiganum. Í 13-stiganum er 00 at skilja sum eitt absolutt null-punkt, sjálvt um tað ikki stendur beinleiðis í kunngerðini, sum sigur, at 00 er eitt undantaksmet, sum verður givið, tá ið einki ella einki fakligt avrik fyriliggur, og fyri at fáa 6 fyri eitt avrik krevst, at avrikið er í minsta lagi 50% av einum fullfíggjaðum avriki. Tað er sostatt ikki av tilvild, at hetta markið er millum 5 og 6, sum er helvtin av 11, ið verður givið fyri eitt fullfíggjað avrik.
Tað absolutta null-punktið er slept í 7-trinstiganum, tí fyrimyndin er ECTS, og har er ikki brúk fyri meira enn tveimum metum, sum verða givin fyri ikki góðkend avrik: eitt, sum vísir, at avrikið var ikki langt frá at verða góðkent, og eitt, har avrikið var so mikið vánaligt, at tað var langt frá at vera góðkent. Tí er –3, sum svarar til F í ECTS-stiganum, eitt met fyri øll avrik, sum eru niðanfyri hetta lágmark, og tað tænir ongum endamáli at hava eitt uppaftur lægri met, sum bara hevði verið brúkt til at traðka á fólk, sum liggja niðri.
Men av tí at miðaltøl skulu roknast eftir 7-trinstiganum, verður tað niðasta metið ein álvarsligur veikleiki, tí nú fáa øll avrik undir eitt vist lágmark –3, og tað telur líka nógv í miðaltalinum, um avrikið er út av lagi vánaligt ella ikki so vánaligt. Eitt 7-tal vigar nú upp ímóti einum –3-tali á sama hátt, sum eitt 9-tal í dag kann viga upp ímóti einum 03.
Hvat skal eitt miðaltal brúkast til?
Fyri at svara hesum spurningi, skulu vit gera okkum greitt, hví vit geva próvtøl. Evaluering í undirvísing og læring hevur tvey høvuðsendamál:
- At fremja læring
- At geva næminginum prógv, sum hann kann brúka sum váttan, tá ið hann søkir inn á aðrar lærustovnar ella søkir starv.
Í tí fyrra endamálinum eru próvtøl sjáldan fremjandi fyri læring, heldur ein forðing. Í tí seinna eru próvtøl eini boð til umheimin, at lærustovnurin váttar, hvat næmingurin dugir. Tað eru eksternir brúkarar, sum lesa hesi prógv og brúka tey til at taka avgerðir eftir.
Kjarnan í spurninginum er, hví vit skulu rokna eitt miðaltal út fyri hesar brúkarar. Duga teir ikki sjálvir at lesa prógvið og gera sær eina meining um tað? Eisini kundi verið spurt, um mediantalið[1] ikki er eitt frægari tal fyri miðjuna av próvtalsbýtinum, enn miðaltalið er. Og um miðaltalið er so áhugavert, er so standardfrávikið[2] ikki eisini áhugavert, so at brúkarin sær, hvussu spjaðingin av metunum er? Tvey prógv við sama miðaltali eru ikki eins, um spjaðingin er ymisk. Hagfrøðingar nýta onkuntíð skemtisøgur at lýsa hetta fyribrigdi. Ein er um mannin, sum hevði annað beini í bakarovninum og annað í frystiboksini, men miðal kropshitin hjá honum var normalur.
Í hægri lærustovnum í Danmark er siðvenja at taka næmingar inn eftir miðaltali, og tí er 7-trinstigin í tølum og ikki bókstavum. Tá ið nýggjur próvtalsstigi skuldi gerast, var annars møguleiki fyri at bróta hesa siðvenju, sum ikki er annað enn ein gomul regla, sum tíðin langt síðani er farin frá. Í hagfrøði er altíð vandi fyri at misnýta tøl, og tá ið miðaltøl verða roknað, er hesin vandi eisini ofta til steðar. Dømi 3 lýsir hetta:
Dømi 3
Ein næmingur fær hesi met eftir 7-trinstiganum: 10, 7, 00, 00, 00 og 00; tað er 2,8 í miðal, og standardfrávikið er 4,5. Ein annar næmingur fær 7, 4, 4, 02, 02 og –3; tað er 2,7 í miðal, og standardfrávikið er 3,3. Eftir miðaltalsregluni er tað fyrra prógvið betri enn tað seinna, hóast tann fyrri er dumpaður í 4 av 6 lærugreinum, og tann seinni er dumpaður í einari av 6. Til samanberingar er mediantalið hjá tí fyrra 0,0; men hjá tí seinna er tað 3,0, sum er nógv betri enn hjá tí fyrra. Dømi 3 vísir tað absurda í at rokna miðaltøl av karakterum.
Ein álvarslig avleiðing av, at miðaltøl hava so stóran týdning eftir miðnám, er, at næmingar velja lærugreinir, har útlit eru fyri góðum metum, heldur enn at velja lærugreinir, sum eru hentar og viðkomandi at hava eftir miðnám. Tær skeivu avgerðirnar sum verða tiknar av myndugleikum og politikarum, fáa næmingarnar at velja taktiskt og flyta fokus frá at læra til at dyrgja eftir góðum miðaltølum. Og vit fáa eitt minni effektivt skúlaverk.
Samanumtikið
- Tann nýggi 7-trinstigin er eitt framstig, tá ið met skulu umsetast til ECTS stigan.
- Tvær vegleiðingar, sum myndugleikarnir hava gjørt um umseting frá 13-stiganum til 7-trinstigan, samsvara ikki: tann vegleiðingin, sum samanber einstøku metini við 13-stigan, er ikki linjubein, men tann, sum samanber miðaltøl frá báðum stigum, hevur linjubeina umrokning.
- 7-trinstigin er ein samanblanding av tveimum prinsippum, sum ikki hóska saman. Annað er siðvenjan í Føroyum at rokna miðaltøl av øllum metum í einum prógvi; og hin er siðvenjan við bókstavsmetum, har miðaltøl ikki skulu roknast.
- 7-trinstigin er eitt afturstig í sambandi við at rokna miðaltøl, tí at miðaltølini verða skeivari enn tey eru við 13-stiganum.
- Tað er at undirmeta próvtalsbrúkarar at rokna eitt miðaltal fyri teir.
- Tað at miðaltøl hava so stóran týdning eftir miðnám, fær næmingarnar at taka skeivar avgerðir um valfak, og útbúgvingin verður minni effektiv.
- Tann europeiski bókstavsstigin hevði verið eitt betri val, tí hann hevði forðað fyri villleiðandi miðaltølum.
Keldur
HOLM-LARSEN, S. OG PLISCHEWSKI, N., 2006, Karakterbekendgørelsen 2006, Kroghs Forlag.
KNIGHT, P., 2002. Summative Assessment in Higher Education: practices in disarray, Studies in Higher Education, Vol. 27, No. 3, pp. 275-286.
UDDANNELSESGUIDEN.dk, Ny karakterskala (Artikel), (niðurtikin 17. desember 2008).
[1] Mediantalið er tað mittasta talið, tá ið øll tølini eru skipað eftir stødd.
[2] Standardfrávikið er eitt tal, sum lýsir spjaðingina av tølunum. Eitt stórt standardfrávik svarar til, at nógvir karakterir eru langt frá miðaltalinum.








